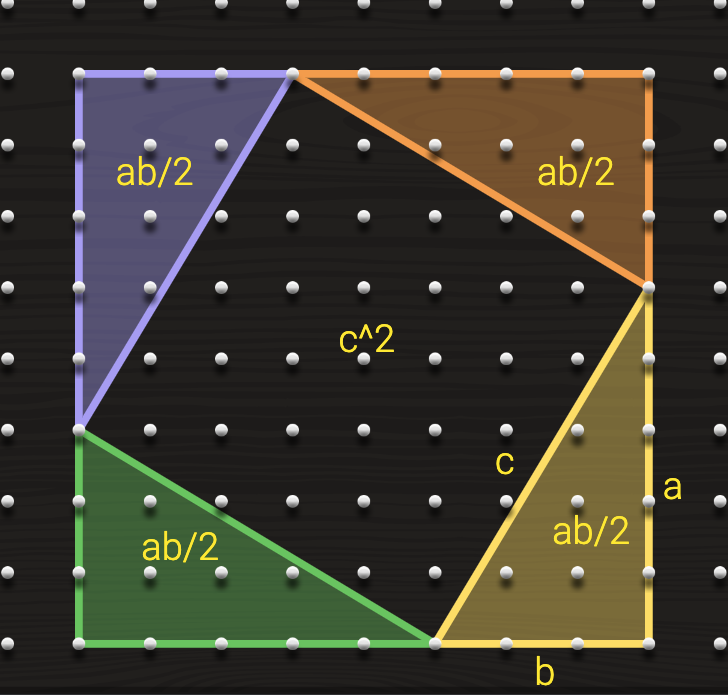
I had a fantastic experience teaching my 8-year-old about the Pythagorean theorem using a Geoboard, we are able to come up a very simple visual proof of the theorem. One can see the area of the outside square is: (a+b)2, but it also equals to 4 right angle triangles (all of them the same size, just different orientation, each triangle has area ab/2) and one small square, whose area is c2 for a total of c2+2ab, hence (a+b)2 = c2 + 2ab, so it's easy to see a2+b2 = c2.
After she learned about square roots using IXL, I was able to show her how to apply the theorem to find the distance between two points on a coordinate system, particularly lattice points.
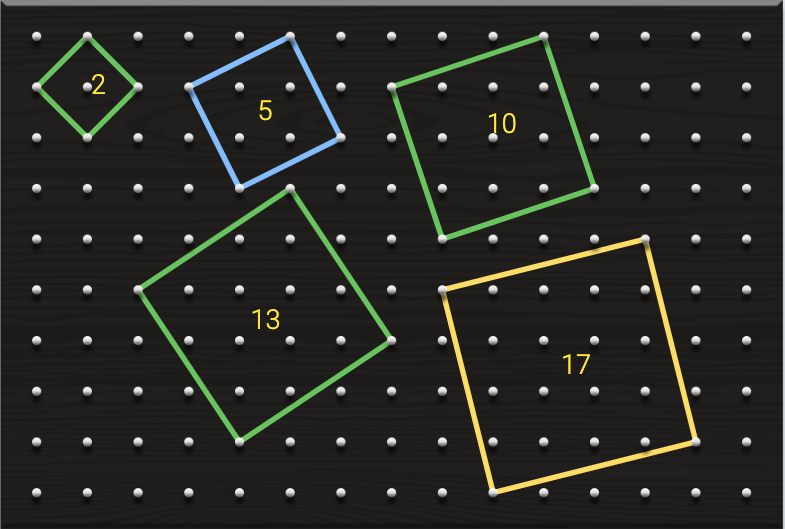
One of the things that Geoboard is good about, is to visually create length of special square root, such as √2, √5, √10, √13, √17, etc... and squares with areas 2, 5, 10, 13, 17, etc. It's really fascinating. My child is eager to solve questions related to square root, which is ranging from grade 9-11 IXL questions. I found out using Geoboard is the best approach.
I used a Geoboard Chrome extension to demonstrate how to use the backtrack algorithm to place 10 points on a 5x5 Geoboard's lattice points in such a way that each row, column, and diagonal would have 2 points. While this may seem complex, I found that using a physical Weiqi board, a Chinese game, made it much easier to execute the backtrack algorithm steps for this particular exercise.



